Identity Dual Operations with 0 and 1 1 X 0 = X (identity) 3 X 1 = 1 (null element) 2 X1 = X 4 X0 = 0 Idempotency theorem 5 X X = XIn the 4 th Chapter of Class 9 RD Sharma Solutions students will study important identities as listed below Algebraic Identities Introduction Identity for the square of a trinomial Sum and difference of cubes Identity These books are widely used by the students who wish to These NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 95 Questions and Answers are prepared by our highly skilled subject experts NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 95 Question 1 Use a suitable identity to get each of the following products
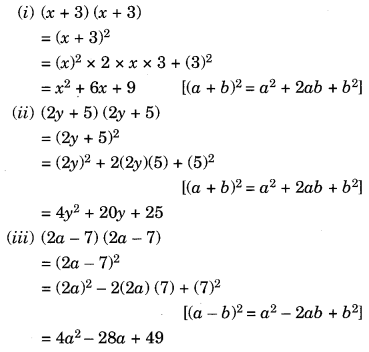
Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Learn Cbse
(x+y)^3 identity class 9
(x+y)^3 identity class 9-18 EXEMPLAR PROBLEMS = 27 9 8 6 33 64 16 × −× − = 0 Since, 3 4 p = 0, so, g(x) is a factor of p(x) Sample Question 2 Find the value of a, if x – a is a factor of x3 – ax2 2x a – 1 Solution 3Let p(x) = x – ax2 2x a – 1 Since x – a is a factor of p(x), so p(a) = 0 ie, a3 – a(a)2 2a a – 1 = 0 a 3 – a 2a a – 1 = 0 3a = 1 = x 2 y 2 z 2 – 6xyz 8 Question 3 Find the following squares by using the identities (i) (b – 7) 2 Solution (b – 7) 2 Using Formula (x – y) 2 = x 2 y 2 – 2xy Putting x = b & y = 7 = b 2 72 – 2(b)(7) = b 2 – 14b 49 (ii) (xy 3z) 2 Solution (xy 3z) 2 Using Formula (a b) 2 = a 2 b 2 2ab Putting a = xy & b




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions
(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5) A Computer Science portal for geeks It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions(a)x39 x2 23x15 (b) x36 x2 11x6 Q3 Factorize the following by using a suitable identity (a) 4x2 12xy 9y2 (b) 2a5 – 54 a2 (c) 22x3 3 3 y3 (d) x5 x (e) x6 – y6 (f) (ab)3 (bc)3 (ca)3 (f) x8y8 (g) 27x3135x2 225x 125 Q4 Evaluate the following using a suitable identity
Examples of expressions are x 3, 2y – 5, 3x 2, 4xy 7 etc You can form many more expressions As you know expressions are formed from variables and constants The expression 2y – 5 is formed from the variable y and constants 2 and 5 The expression 4xy 7 is formed from variables x and y and constants 4 and 7 This video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuserie Multiply the following expressions (a) 3xy 2 × (5x 2 y) (b) x 2 yz × xy 2 z × x 2 yz Solution Question 9 Find the area of the rectangle whose length and breadths are 3x 2 y m and 5xy 2 m respectively Solution Length = 3x 2 y m, breadth = 5xy 2 m Area of rectangle = Length × Breadth = (3x 2 y × 5xy 2) sq m = (3 × 5) × x 2 y × xy
Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y) So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy (x y) = (x y) (x y)2 – 3xy) Using (ab)2 = a2 b2 2ab = (x y) (x2 y2 2xy) – 3xy = (x y) (x2 y2 – xy) = (x y) (x2 xy y2) = RHS RHS (x y) (x2 – xy y2) Hence provedFactor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)1 Identify the terms, their coefficients for each of the following expressions In the expression 5xyz 2 – 3zy, the terms are 5xyz 2 and –3zy coefficient of xyz 2 in the term 5xyz 2 is 5 coefficient of zy in the term –3zy is –3 In the expression 1 x x 2, the terms are 1, x and x 2
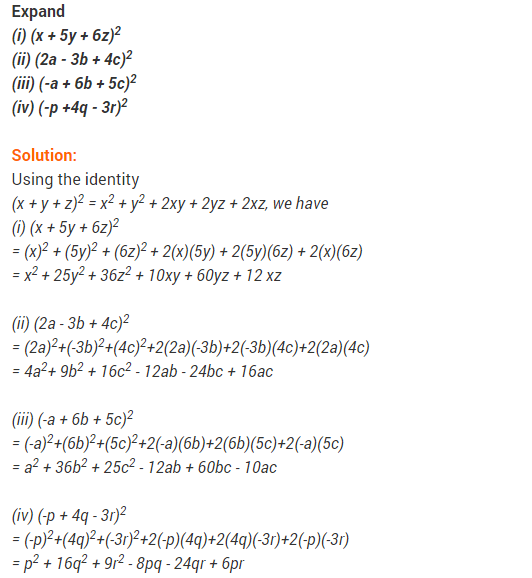



Polynomials Class 9 Extra Questions Maths Chapter 2 Learn Cbse




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Updated For 21 22 Coolgyan Org
CLASSIX MATHEMATICS ASSIGNMENT2 CHAPTER – 2 POLYNOMIALS SECTIONA 1 Write the degree of the given polynomials i) ( 2x 4 )3 ii) ( t3 4 ) ( t3 9 ) 2 Write the coefficient of x4 and x in 4x3 5x4 2x2 3 3 Find the zeroes of f(z)=z2 2z 4 Find the product using suitable identities (4 5x)(45x) 5 WhatProblem Solve (x 3) (x – 3) using algebraic identities Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of
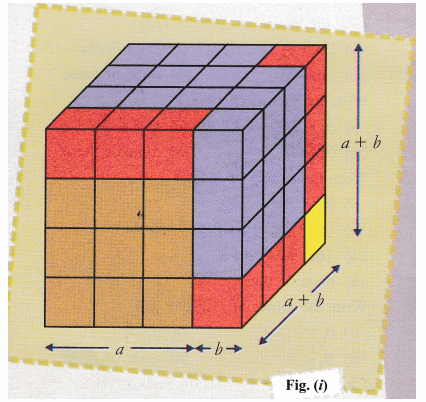



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5
The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3 Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0 If x/2 y3/b2 z3/c2 = (x y z)3/(a b c)2 asked in Class X Maths by priya12 Expert ( 749k points) ratio and proportion




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Exercise 9 5
Rs Aggarwal 19 Solutions for Class 9 Math Chapter 3 Factorisation Of Polynomials are provided here with simple stepbystep explanations These solutions for Factorisation Of Polynomials are extremely popular among Class 9 students for Math Factorisation Of Polynomials Solutions come handy for quickly completing your homework and preparing for exams Chapter 9 NCERT Solutions will be very useful in preparation of the examinations and understanding the concepts properly 1 Identify the terms, their coefficients for each of the following expressions Coefficient in 5xyz 2 is 5 and in 3zy is 3 Coefficient of x and of x 2 is 1 (iii) Terms 4x 2 y 2 , 4x 2 y 2 z 2 and z 2 Question 4 What is the value of a if 2x² x – a is equal to 5 and x = 0 Question 5 Simplify the expression 2 (a² ab) 3 – ab and find its value when a = 5 and b = – 3 Question 6 Using proper identity, find the value of (12)² – (08)² Question 7 Question 8




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 4 Ncert Solutions




Polynomials Important Questions Of Identities Algebraic Identities Class 9 Oda Class Youtube
Hope the information shed above regarding NCERT MCQ Questions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities with Answers Pdf free download has been useful to an extent If you have any other queries of CBSE Class 8 Maths Algebraic Expressions and Identities MCQs Multiple Choice Questions with Answers, feel free to reach us so Students can also refer to NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities for better exam preparation and score more marks Algebraic Expressions and Identities Class 8 MCQs Questions with Answers Question 1 The expression x 3 is in (a) one variable (b) two variables (c) no variable (d) none of these Answer Identity VII is a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) Lets take an example a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) 2 3 3 3 4 3 – 3(2)(3)(4) Chapter 3 Class 9 Coordinate Geometry (Term 1) →




Rd Sharma Solutions For Class 9 Mathematics Cbse Chapter 5 Factorisation Of Algebraic Expressions Topperlearning




Algebraic Identities Of Polynomials A Plus Topper
Xy 2 cos x y 2 sinx siny= 2sin x y 2 cos xy 2 cosx cosy= 2cos xy 2 cos x y 2 cosx cosy= 2sin xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If a Telangana SCERT Solution Class IX (9) Math Chapter 2 Polynomials and Factorisation Exercise 25 = on comparing it with (ab) (ab) we get Hence 4x 3y is the factor of the above equation Hence 2y 1 is the factor of the above sum ∴ (5x 4y 2z) is a factor of the above given sum ∴ (3a 2b – 4c) is a factor of the above given sumAnswer In the given problem, we have to simplify the value of each expression (i) Given We shall use the identity for each bracket x 2 2 y 3 2 z 4 2 2 x 2 y 3 2 y 3 z 4 2 x 2 z 4 By arranging the like terms we get Now adding or subtracting like terms, Hence the value of




Pin By Bontle Masinge On School Polynomials Math Mathematics




Polynomials Class 9 Extra Questions Maths Chapter 2 Learn Cbse
(X Y)3 − (X − Y)3 Can Be Factorized as CBSE CBSE (English Medium) Class 9 Textbook Solutions 9959 Important Solutions 1 Question Bank Solutions 9000 Concept Notes & Videos 309 Syllabus Advertisement Remove all ads (X Y)3 − (X − Y)3 Can Be Factorized as MathematicsWe already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown above3Here, the identity, (x – 3y) = x3 – y – 3xy(x – y) is used (v) 7p3– (1/216)−(9/2) p2(1/4)p Solution The expression, 27p3–(1/216)−(9/2) p2(1/4)p can 2be written as (3p)3–(1/6)3–3(3p)2(1/6)3(3p)(1/6) 27p3–(1/216)−(9/2) p2(1/4)p 2= (3p)3–(1/6)3–3(3p)2(1/6)3(3p)(1/6) = (3p–16)3 = (3p–16)(3p–16)(3p–16) 9



What Is The Formula Of Math A B 3 Math Quora




Rd Sharma Solutions For Class 9 Mathematics Cbse Chapter 4 Algebraic Identities Topperlearning
Learn Algebraic Identities Cubic Type Class 9 through video lessons, MCQs & more at TopperLearning Sign up & access study material of all CBSE Class 9 Mathematics chapters Extra Questions for Class 9 Maths Polynomials with Answers Solutions Extra Questions for Class 9 Maths Chapter 2 Polynomials with Solutions Answers Polynomials Class 9 Extra Questions Very Short Answer Type Question 1 Factorise 125x 3 – 64y 3 Solution 125x 3 – 6443 = (5x) 3 – (4y) 3 By using a3 – b3 = (a – b) (a 2 ab b 2= (x y)(x 2 y 2 2xy x 2 xy y 2) using identity, (a b) 2 = a 2 b 2 2 ab) = (x y) (3xy) Hence, one of the factor of given polynomial is 3xy Question 18 The coefficient of x in the expansion of (x 3) 3 is (a) 1 (b) 9 (c) 18 (d) 27 Solution (d) Now, (x 3) 3 = x 3 3 3 3x (3)(x 3) using identity, (a b) 3 = a 3 b 3
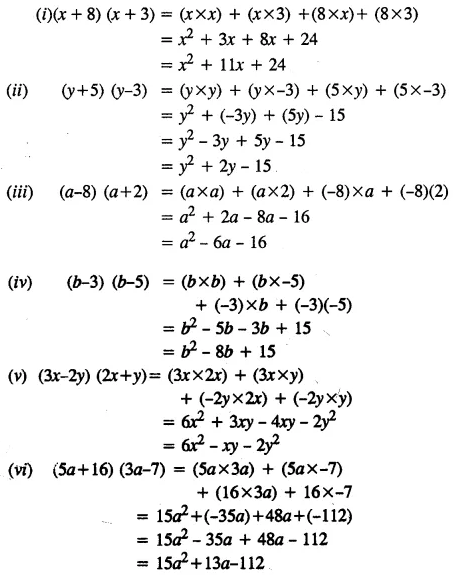



Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts



Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks
Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the otherRD Sharma Mathematics Class 9 Solutions Chapter 4 Algebraic Identities Ex 44 Question 1 Find the following products (i) (3x 2y) (9X 2 – 6xy Ay 2) (ii) (4x – 5y) (16x 2 xy 25y 2) (iii) (7p 4 q) (49p 8 – 7p 4 q q 2) Solution Question 2 If x = 3 and y = 1, find the values of each of the following using in identityThe cube of a plus b is also equal to the a cubed plus b cubed plus three times product of a squared and b plus 3 times product of a and b squared ( a b) 3 = a 3 b 3 3 a 2 b 3 a b 2 In mathematics, the a plus b whole cubed algebraic identity is called in the following three ways The cube of sum of two terms rule



1




Algebraic Identities Of Polynomials A Plus Topper
= (x – y)(x y)(x 2 y 2){(x 2 y 2) 2 – (√2xy) 2} = (x – y)(x y)(x 2 y 2 )(x 2 y 2 – √2xy)(x 2 y 2 √2xy) The document Algebraic Identities Polynomials, Class 9, Mathematics Notes Class 9 is a part of Class 9 categorySolution Verified by Toppr We know the identity a 3−b 3=(a−b)(a 2b 2ab) Using the above identity, the equation x 6−y 6 can be factorised as follows x 6−y 6=(x 2) 3−(y 2) 3=(x 2−y 2)(x 2) 2(y 2) 2(x 2×y 2)=(x−y)(xy)(x 2y 2xy)(x 2y 2−xy)NCERT solutions for Class 8 Maths chapter 9 (Algebraic Expressions and Identities) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear your confusions, if any




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Algebraic Identities Of Polynomials A Plus Topper
NCERT Solution For Class 9 Maths Chapter 2 Polynomials Exercise 25 Page 48 1 Use suitable identities to find the following products Here, the identity, 3 (x y) = x 3 y 3 3xy (x y) is used (ii) 8a 3 –b 3 –12a 2 b6ab 2 Solution The expression, 8a 3 –b 3 −12a 2 b6ab 2 2can be written as (2a) –b 3 –3 Q4 Expand each of the following, using suitable identities (i) (x 2y 4z) 2 (ii) (2x – y z) 2 (iii) (–2x 3y 2z) 2 (iv) (3a – 7b – c) 2 (v) (–2x Students can access the NCERT MCQ Questions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities with Answers Pdf free download aids in your exam preparation and you can get a good hold of the chapter




Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Ncert Solutions For Class 9 Mathematics Maharashtra Chapter 9 Algebraic Expressions And Identities Topperlearning
Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 25 We have created Step by Step solutions for Class 9 maths to help you to revise the18 x 3 – y 3 = (x – y)(x 2 xy y 2) 19 x 2 y 2 z 2 − xy – yz –zx = 1/2(x − y) 2 (y − z) 2 (z − x) 2 Maths Algebraic Identities for Class 9X 3, 2y – 5, 3x2, 4xy 7 etc You can form many more expressions As you know expressions are formed from variables and constants The expression 2 y – 5 is formed from the variable y and constants 2 and 5 The expression 4 xy 7 is formed from variables x and y and constants 4 and 7




Standard Identities Of Binomials And Trinomials Equations Examples




Algebra Formulas For Class 9 Pdf Important Formulas Embibe
(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzClass 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y) ( x a) ( x b) = x2 ( a b) x ab (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Ncert Solutions For Class 8 Mathematics Chapter 9 Algebraic Expressions And Identities Exercise 9 5




Algebraic Identities Of Polynomials A Plus Topper
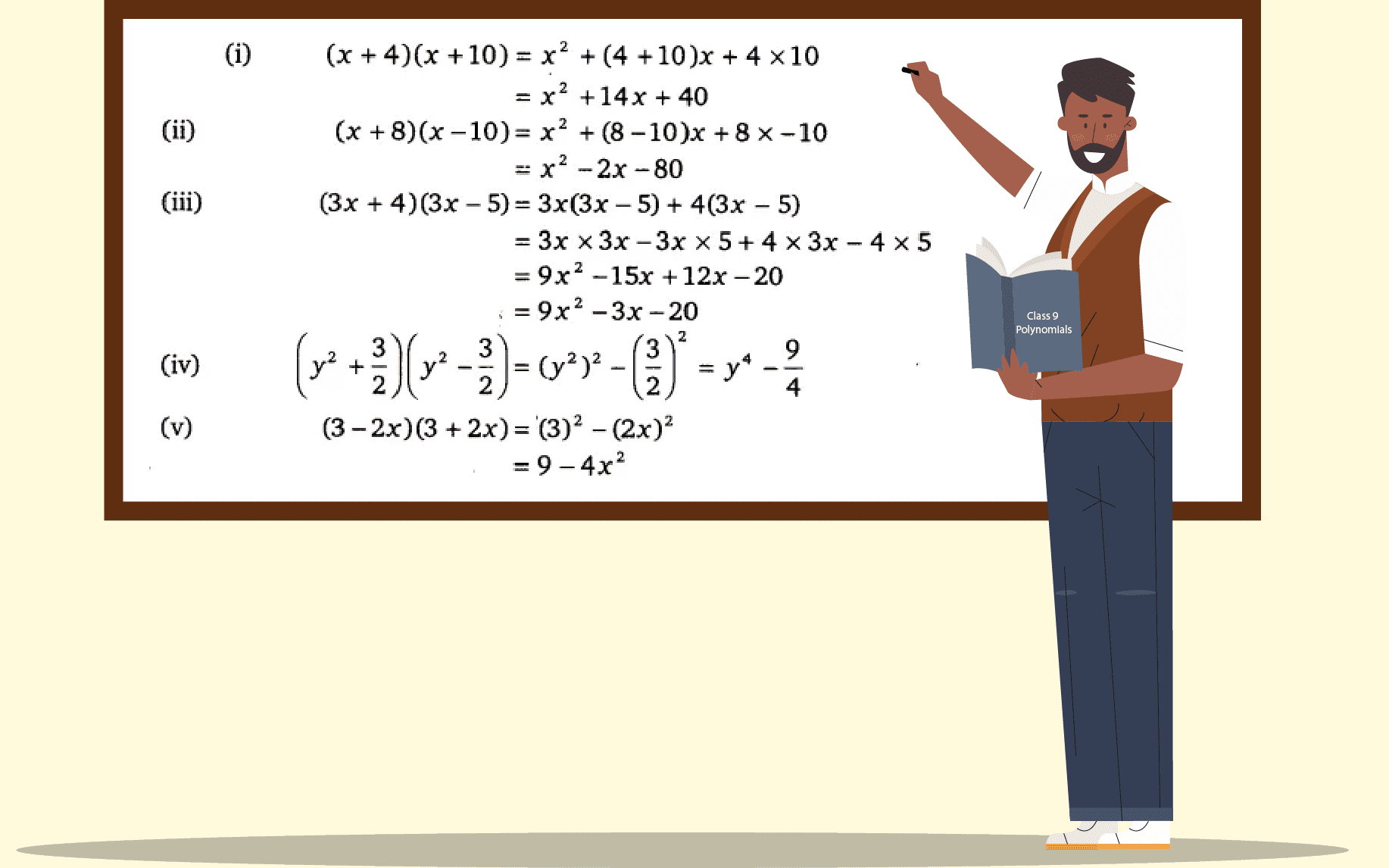



Class 9 Polynomials Study Notes And Important Questions Leverage Edu




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Matrix Multiplication Part Iv Final Part Class 9 Optional Maths Online Class Youtube



1




Cbse Class 8 Maths Chapter 9 Algebraic Expressions And Identities Revision Notes
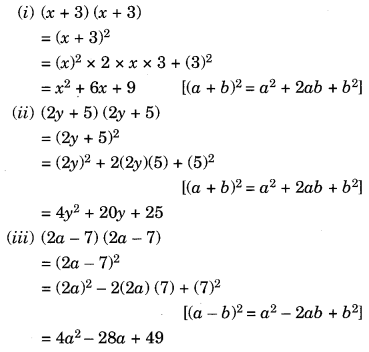



Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Learn Cbse




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Cbse Class 9 Algebraic Identities Offered By Unacademy




Cbse Revision Notes For Class 8 Chapter 9 Algebraic Expressions And Identities




Rd Sharma Class 9 Solutions Chapter 5 Factorisation Of Algebraic Expressions Exercise 5 1




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Bestpixtajpm1d3 ダウンロード済み Factorise X X 3 Y 3 3xy X Y




Using Suitable Identities Find X Y 3 P 2




Algebraic Identities Worksheet




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities




Exercise 25 Question 1 Use Suitable Identities To Find The Following Products X 4 X 10x 8x 10 I 3 3 3x 43x 5 Iii 2 Iv 3 2x 3 2x V Answer I By Using The Identity X Ax B X A B




Algebra Formulas For Class 9 Pdf Important Formulas Embibe




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo
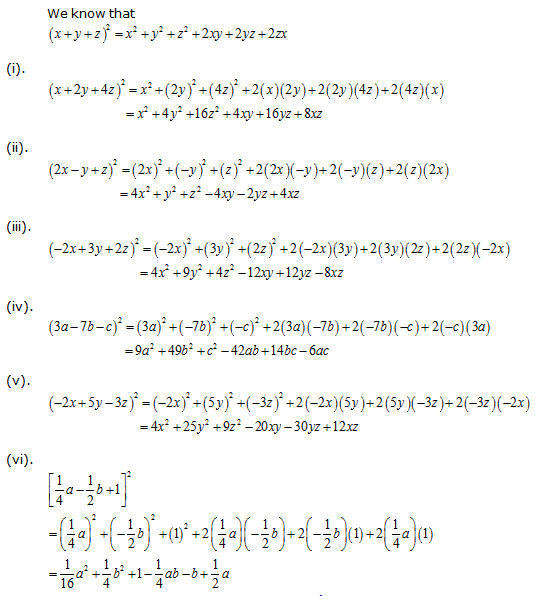



Ncert Solutions For Class 9 Mathematics Cbse Chapter 2 Polynomials Topperlearning




Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com




Ncert Solutions For Class 9 Maths Exercise 2 5 Chapter 2 Polynomials Study Path




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions




Ncert Solutions For Class 7 Maths Chapter 12 Algebraic Expressions




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Algebraic Identities Rd Sharma Class 9 Solutions Exercise 4 5




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials Free Pdf Download Esaral




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com




Polynomials Class 9 Notes Maths Chapter 2 Learn Cbse




Verify X3 Y3 And X3 Y3 Std 9 Maths Ex 2 5 Q 9 Youtube



Cbse Class 8 Mathematics Algebraic Identities Bridge Course Worksheet
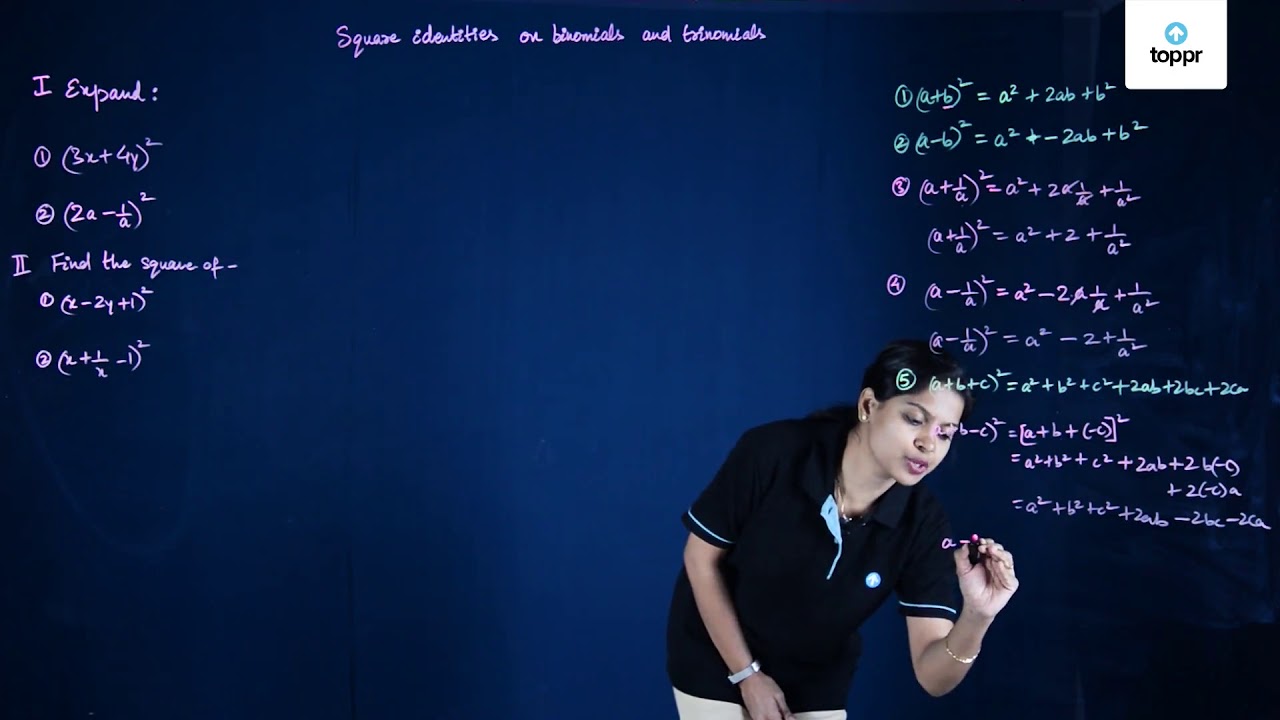



Standard Identities Of Binomials And Trinomials Equations Examples



1



Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks
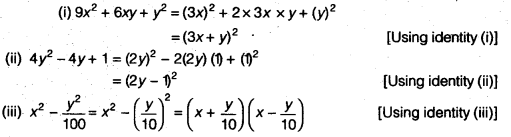



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Ex 9 5 3 Find B 7 2 Using Algebra Identities Teachoo



Polynomials Class 9 Worksheet Pdf
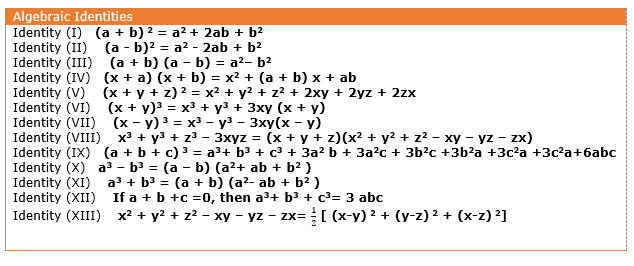



All Useful Algebraic Identities With Proof Examples Physicscatalyst S Blog




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Ex 2 5 3 I Factorise 9x2 6xy Y2 Using Appropriate Identities



Class 10 Class 9 Algebraic Identities




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf




All Identities Of Class 9 Maths Ch 2 Polynomial Brainly In
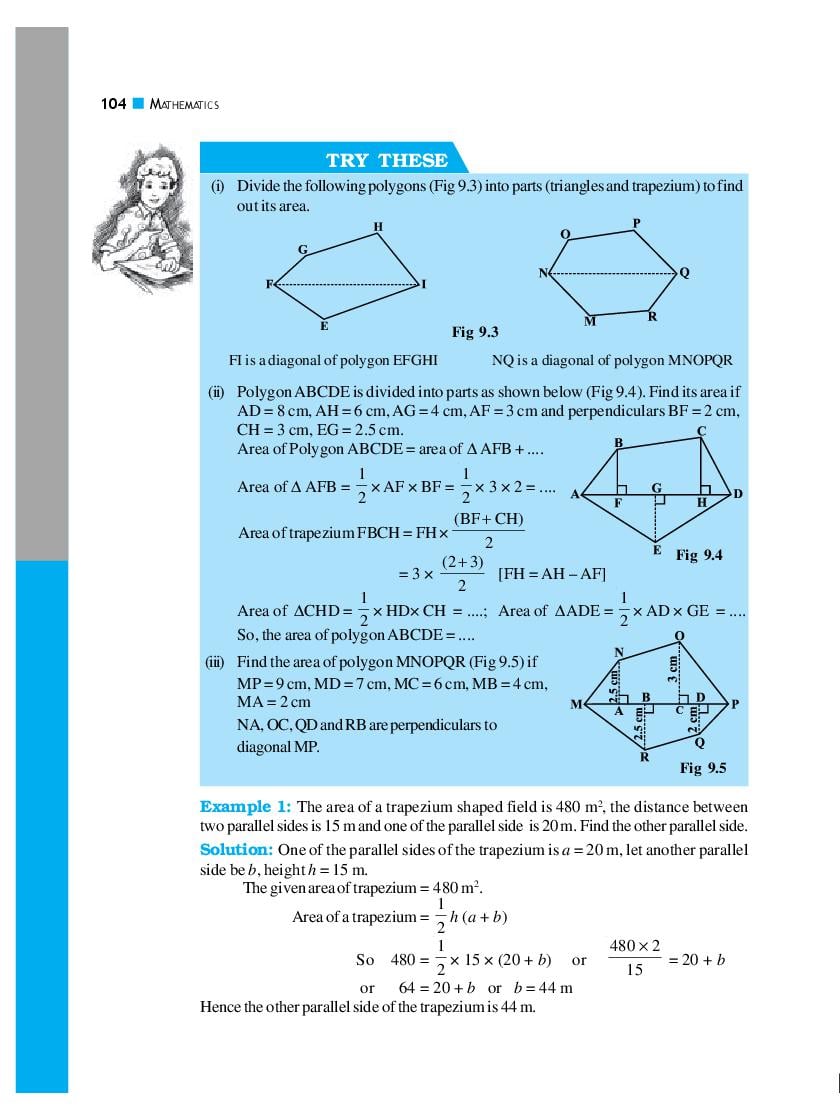



Ncert Book Class 8 Maths Chapter 9 Algebraic Expressions And Identities




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In



Grubosc Doktor Filozofii Mysz Lub Szczur X 3 Y 3 Cholera Przodek Patrol




Ncert Solutions For Class 9 Mathematics Maharashtra Chapter 9 Algebraic Expressions And Identities Topperlearning




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




Rd Sharma Solutions For Class 9 Mathematics Cbse Chapter 4 Algebraic Identities Topperlearning



Ncert Solutions Class 8 Mathematics Algebraic Expressions And Identities




Algebraic Identities Of X Y And X Y 3 Mins




Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities




Cbse Class 8 Mental Maths Algebraic Expressions And Identities Worksheet
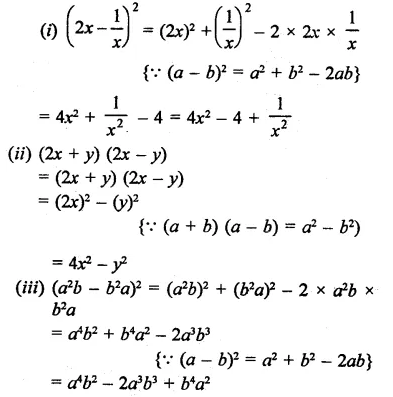



Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4 1




Notes Of Ch 2 Polynomials Class 9th Math




Rs Aggarwal Class 9 Solutions Chapter 3 Factorisation Of Polynomials



Rd Sharma Solutions Class 9 Chapter 4 Algebraic Identities



Rd Sharma Solutions Class 9 Chapter 4 Algebraic Identities



Maths Formulas For Class 9 Cbse Chapter 3 Coordinate Geometry




Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities



Cbse Class 9 Maths Lab Manual Algebraic Identity A3 A B Ab B2 Cbse Sample Papers




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf
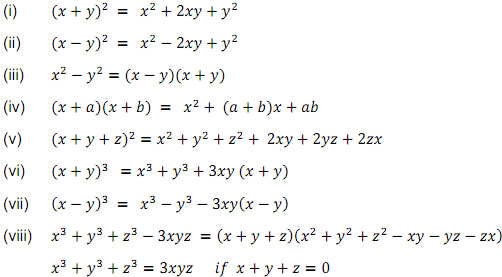



Maths Formulas For Class 9 Cbse Chapter 3 Coordinate Geometry
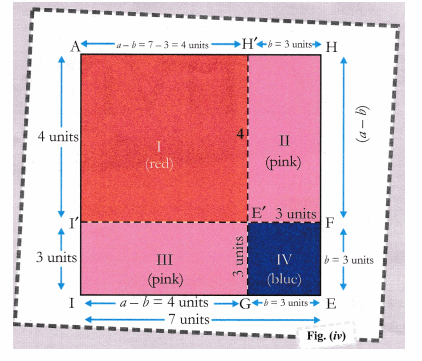



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers



Cbse Class 8 Maths Algebraic Expressions And Identities Hots




If X 2 Y 2 49 And X Y 3 Then Find The Value Of X 3 Y 3



0 件のコメント:
コメントを投稿